ivan wrote:I like mlepage's approach, it's clear and fast.
No variable arguments, no function calls, no intermediate tables or objects:
[...]
Tahel/vrld approach is ok - it uses "math.min" and "math.max"
but works slower since these functions accept variable arguments.
Robin's method is cool but it creates an intermediate table and table.sort
would probably be slower for common cases with 2 arguments.
Oh yeah?
Code: Select all
function clamp_one(v, a, b)
assert(a <= b, "invalid clamp range") -- optional: debug message
if v < a then
v = a
elseif v > b then
v = b
end
return v
end
function clamp_two(v, a, b)
if v < a then
v = a
elseif v > b then
v = b
end
return v
end
function clamp_two_and_a_half(v, a, b)
if v < a then
return v
elseif v > b then
return b
end
return v
end
function clamp_three(v, a, b)
return math.max(a, math.min(v, b))
end
local min, max = math.min, math.max
function clamp_four(v, a, b)
return max(a, min(v, b))
end
function clamp_now_thats_just_silly(...)
local s = {...}
table.sort(s)
return s[2] --fixed //thelinx
end
function clamp_verbose(a, b, c)
return (a < b and b < c and b) or (c < b and b < a and b) or (a < b and c < b and c) or (b < a and a < c and a) or c
end
function clamp_the_hard_way(low, num, high)
local s = string
local digitLength = s.len( math.floor(high) )
local function c(n, p)
return unpack( -- it's not a party without unpack and string.format
{ s.byte ( -- convert to ASCII code
s.format( "%0"..digitLength..".0f", n )
, p ) +2 } -- "0" is 48 and "9" is 57, so to align it, +2 is needed
)
end
if c(high,i) < c(num,i) then -- if the first digit of high is < num's digit
return high
end
for i = 1, digitLength do -- one at a time, going from left to right
local l, n = c(low,i), c(num,i) -- arrange numbers to evenly, get one digit from each
if l > n then return low -- compare them
elseif l < n then return num
end -- if they're both equal, proceed to next digit
end
return num -- low and num were entirely equal
end
function time(f, N)
local dts = {}
for i = 1,N or 2000000 do
local t = love.timer.getTime()
f(math.random(), math.random(), math.random()+1)
dts[#dts+1] = love.timer.getTime() - t
end
local t = 0
for _, dt in ipairs(dts) do
t = t + dt
end
local dt_mean = t / #dts
local dt_std = 0
for _, dt in ipairs(dts) do
dt_std = dt_std + (dt_mean - dt) ^2
end
dt_std = math.sqrt(dt_std / (#dts-1))
print((" spent %ss in %d calls (%ss +- %ss per call)"):format(t, #dts, dt_mean, dt_std))
end
function love.load()
love.timer.sleep(1)
print("if-else with assert")
time(clamp_one)
print("\nif-else without assert")
time(clamp_two)
print("\nif-else without assert early out")
time(clamp_two_and_a_half)
print("\nmath.max/math.min")
time(clamp_three)
print("\nmath.max/math.min localized")
time(clamp_four)
print("\ntable.sort")
time(clamp_now_thats_just_silly)
print("\nlazy logic")
time(clamp_verbose)
print("\nstring compare")
time(clamp_the_hard_way)
love.event.quit()
end
Output (shortened)
Code: Select all
if-else with assert
spent 0.93s in 2000000 calls (4.65e-07s +- 1.35e-07s per call)
if-else without assert
spent 0.93s in 2000000 calls (4.67e-07s +- 1.24e-07s per call)
if-else without assert early out
spent 0.95s in 2000000 calls (4.75e-07s +- 1.35e-07s per call)
math.max/math.min
spent 0.98s in 2000000 calls (4.88e-07s +- 1.17e-07s per call)
math.max/math.min localized
spent 0.94s in 2000000 calls (4.69e-07s +- 1.25e-07s per call)
table.sort
spent 1.49s in 2000000 calls (7.46e-07s +- 8.85e-06s per call)
lazy logic
spent 0.94s in 2000000 calls (4.69e-07s +- 1.16e-07s per call)
string compare
spent 9.97s in 2000000 calls (4.99e-06s +- 1.45e-05s per call)
Here is a chart of the mean time and and the standard deviation of the time for each test case:
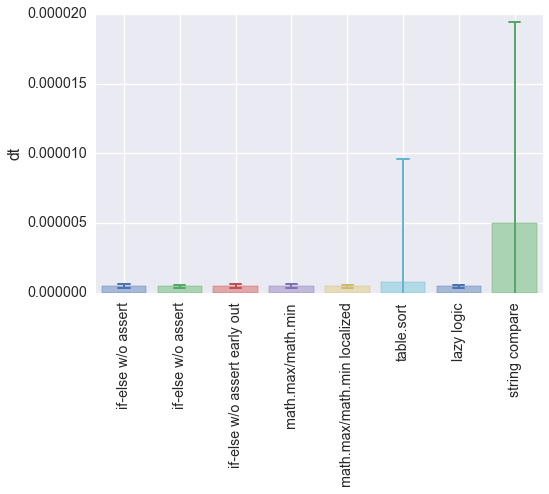
- timeplot.png (26.02 KiB) Viewed 5674 times
Here is a closer look:
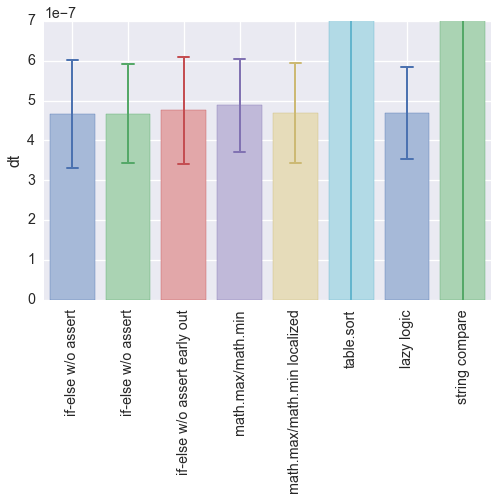
- timeplot-serious.png (25 KiB) Viewed 5674 times
None of the serious solutions is significantly faster than any other.
The lesson? Measure before you assume.